#define MAX(X, Y) (((X) > (Y)) ? (X) : (Y))
MAX(a++, b++) // (((a++) > (b++)) ? (a++) : (b++))
MAX(0, "123") // runtime errorModern C++模板元编程
template <typename 😀>
Netcan 2022-09-04 @Shanghai
自我介绍
96年出生,18年毕业于合肥工业大学本科
某大厂高级工程师
机工社 《C++20高级编程》作者
知乎 《魅力C++》 专栏作者
兴趣:CS, OO, FP, Design, Coding, Writing
Skills: C/C++/Rust, Haskell/Scheme, Bash/Python
议程
什么是模板元编程
模板历史
元编程与函数式编程范式
元编程基石TypeList,原子操作Map/Filter/Fold
模板元编程实战
快速排序
图DSL:全局最短路径
结论
模板介绍
起初为了支持泛型替代宏而设计的语法
类型安全,编译期提前检查错误
人们无意中发现可以用于 编译期 计算
语言标准发展不断完善元编程体验
泛型算法 & 宏
void qsort( void *ptr, size_t count, size_t size,
int (*comp)(const void *, const void *) );int values[] = { 88, 56, 100, 2, 25 };
int cmpfunc (const void* a, const void* b) {
return ( *(int*)a - *(int*)b );
}
qsort(values, 5, sizeof(int), cmpfunc);泛型算法 & 模板函数
template<typename T>
T max(T&& a, T&& b) {
return a > b ? a : b;
}max(0, "123"); // error: no matching function for call to 'max(int, const char [4])'template<typename RandomIt, typename Compare>
void sort(RandomIt first, RandomIt last, Compare comp);int values[] = { 88, 56, 100, 2, 25 };
std::sort(values, values + 5, [](int a, int b) {
return a < b;
});泛型容器 & 宏
// collection.h
struct Collection_ ## TYPE {
TYPE *array; (1)
size_t size, n;
};
#ifdef INSTANCE (2)
Collection_ ## TYPE make_Collection_ ## TYPE(size_t sz) {
// ...
}
#endif| 1 | 类型参数 TYPE |
| 2 | 实例化函数 |
泛型容器 & 宏
// main.cpp
#define INSTANCE
#define TYPE int (1)
#include "collection.h"
#undef TYPE
#define TYPE double(1)
#include "collection.h"
#undef TYPE
int main() {
Collection_int lstInt = make_Collection_int(5); (2)
Collection_double lstDouble = make_Collection_double(5);
}| 1 | 实例化类型 Collection_int, Collection_double |
| 2 | 实例化成员函数 |
| 这也称为预处理多态技术 |
泛型容器 & 模板
// collection.h
template <typename T> (1)
class Collection {
T* array;
size_t size, n;
public:
Collection(size_t sz) {
// ...
}
};
// main.cpp
int main() {
Collection<int> lstInt(5); (2)
Collection<double> lstDouble(5); (2)
}| 1 | 模板参数 T |
| 2 | 实例化类型 Collection<int>, Collection<double> |
零成本抽象
C++ implementations obey the zero-overhead principle: What you don’t use, you don’t pay for. And further: What you do use, you couldn’t hand code any better.
— Bjarne Stroustrup
元编程 & Metaprogramming
编译器解析执行代码,并 生成 代码、数据
将运行时逻辑挪到编译时计算,实现零成本抽象
运行时拥有改变结构的能力,动静结合
元编程 & 流派
模板元编程
两者结合
Constexpr all the things!

模板元编程
运行时交互
数值
对象
编译时计算(常量)
数值
类型
对象 (C++20)
模板元编程
函数式编程范式
无副作用纯函数,Immutable
延迟计算
模式匹配
模板元编程:数值计算
计算Fibonacci数列: \$f(n) = f(n-1) + f(n-2)\$
template <size_t N> (1)
struct Fibonacci { (2)
constexpr static size_t value = (3)
Fibonacci<N - 1>::value +
Fibonacci<N - 2>::value;
};
template <> struct Fibonacci<0> { (4)
constexpr static size_t value = 0;
};
template <> struct Fibonacci<1> { (4)
constexpr static size_t value = 1;
}
template<size_t N>
constexpr size_t Fibonacci_v = Fibonacci<N>::value; (5)| 1 | 模板元函数 输入 参数N,size_t 表明输入参数为 值 |
| 2 | 模板元函数名 Fibonacci |
| 3 | 模板元函数 输出 返回 值 value |
| 4 | 模式匹配,函数递归的边界条件 |
| 5 | 别名,方便调用 |
如何调用
Fibonacci<10>::value // 55
Fibonacci_v<10> // 551. 约定 尖括号 为模板元函数F调用,value 作为函数的 返回值2. 模板元函数名后缀 _v 为其别名: F_v<IN> ,避免写一长串 F<IN>::value 的烦恼 |
模板元编程:类型计算
计算类型 T 的指针类型 T*
template <typename T> (1)
struct AddPointer { (2)
using type = T*; (3)
};
template <typename T>
using AddPointer_t =
typename AddPointer<T>::type; (4)| 1 | 模板元函数 输入 类型T,typename 表明输入参数是 类型 |
| 2 | 模板元函数名 |
| 3 | 模板元函数 输出 返回 类型 type |
| 4 | 别名,方便调用 |
如何调用
typename AddPointer<int>::type px =
new int{5};
AddPointer_t<int> px2 = new int{5};1. 约定 尖括号 为模板元函数F调用,type 作为函数的 返回类型2. 模板元函数名后缀 _t 为其别名: F_t<IN> ,避免了写一长串 typename F<IN>::type 的烦恼 |
模板元编程:基础数据类型
复合数据类型:TypeList
输入多个 类型 参数:T1, T2, …
输出一个 TypeList 类型
template <typename ...Ts> (1)
struct TypeList {
using type = TypeList<Ts...>; (2)
constexpr static size_t size = sizeof...(Ts); (3)
};| 1 | 输入参数,…Ts 模板参数包 声明,表示接收任意多的类型参数: T1, T2, T3, … |
| 2 | 输出类型,Ts… 表示展开 模板参数包,展开后为T1, T2, T3, … |
| 3 | 列表长度,sizeof… 操作符求参数包个数 |
值与类型
using BoolSet = TypeList<true, false>; // template argument for template type parameter must be a type什么是值
值是常量
什么是类型
类型是值的集合
值与类型如何转换
一一映射,就能相互转换
template<typename T, T v> (1)
struct integral_constant {
constexpr static T value = v; (2)
};| 1 | 指定类型,与具体的值 |
| 2 | 存储其值 |
值转换成类型:
using true_type = integral_constant<bool, true>;
using false_type = integral_constant<bool, false>;类型转换成值:
true_type::value // true
false_type::value // false融入类型体系
using BoolSet = TypeList<true_type, false_type>; // OkTypeList
基本操作
向TypeList尾部插入一些类型:
append类型参数转发:
exportTo高阶函数
MapFilterFold
append
向TypeList尾部插入一些类型
template <typename ...Ts>
struct TypeList {
template <typename ...T> (1)
using append = TypeList<Ts..., T...>; (2)
};| 1 | 输入一些需要插入的类型参数 T… |
| 2 | 输出插入类型之后的TypeList |
如何调用
TypeList<int, char>::append<long, double> // TypeList<int, char, long, double>exportTo
类型参数转发
将 TypeList<Ts…> 参数转发至其他模板类,例如转成: std::tuple<Ts…>
template <typename ...Ts>
struct TypeList {
template <template<typename...> typename T> (1)
using exportTo = T<Ts...>; (2)
};| 1 | 输入一个模板类 T |
| 2 | 输出转发类型参数后的模板类 T<Ts…> |
template<typename …> typename T 表示模板类 T 接收可变类型参数 |
如何调用
TypeList<int, char>::exportTo<std::tuple> // std::tuple<int, char>
TypeList<int, char>::exportTo<std::variant> // std::variant<int, char>高阶函数
数学和计算机科学定义如下高阶函数:
输入的参数为函数
输出的参数为函数
常用到的有:
template<typename RandomIt, typename Compare>
void sort(RandomIt first, RandomIt last, Compare comp); (1)| 1 | sort为高阶函数,其输入参数为 comp 函数 |
Map高阶函数
输入一个列表和函数 f
输出对列表中的每个元素进行f函数调用后的列表
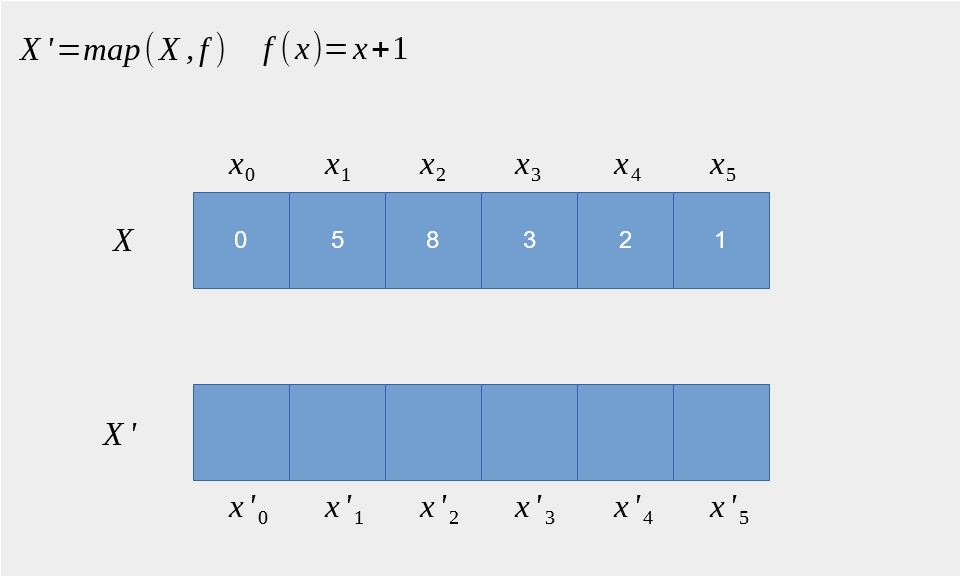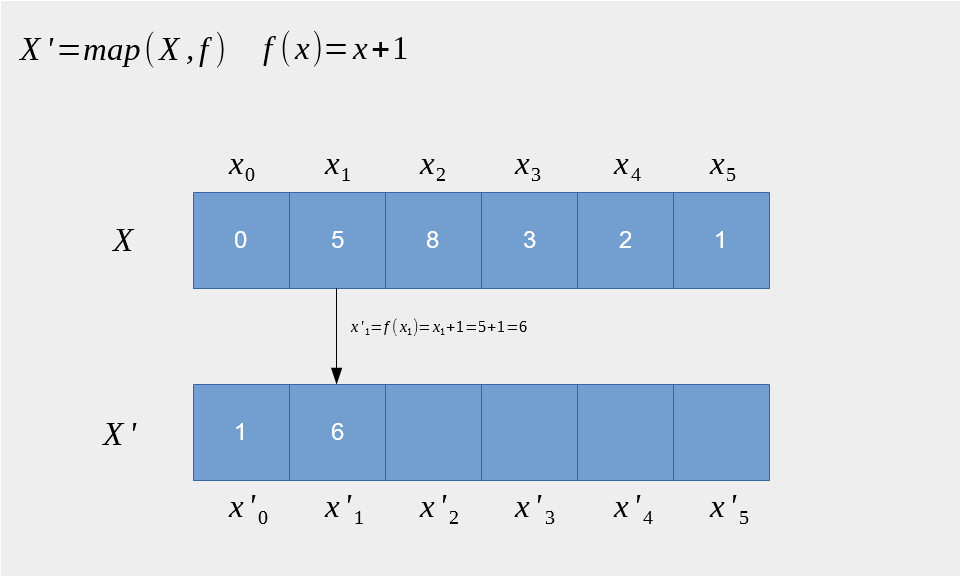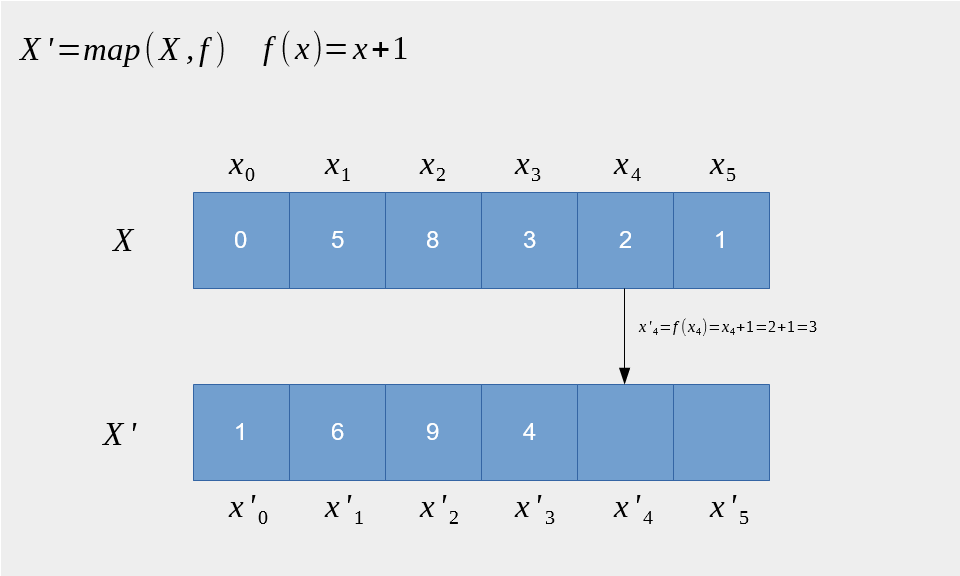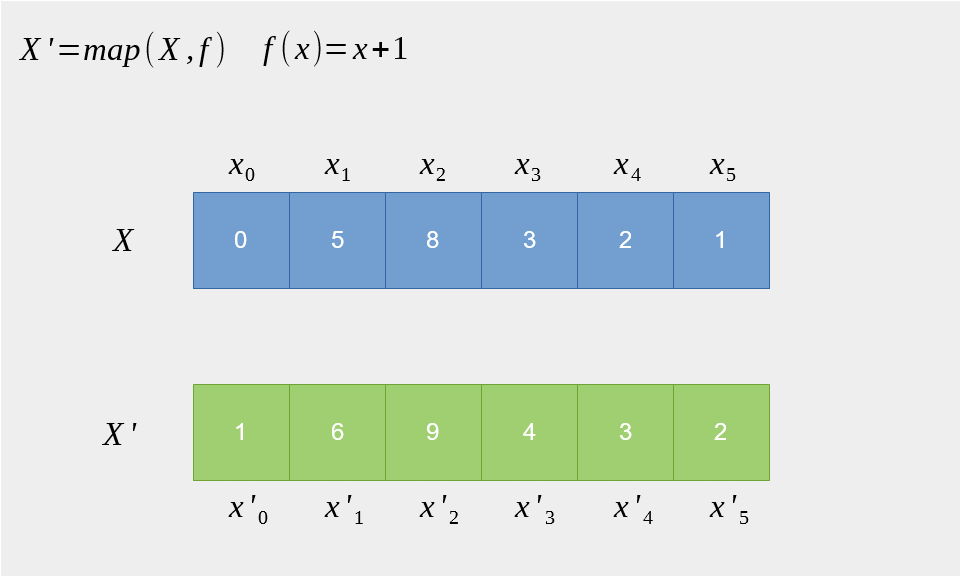
Filter高阶函数
输入一个列表和谓词函数P
对列表中的每个元素进行过滤操作,输出只保留谓词函数为真的元素的列表

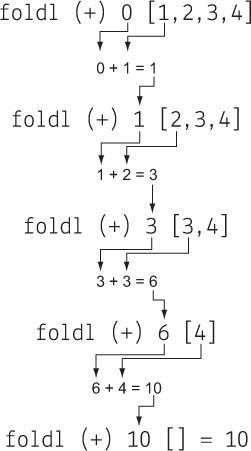
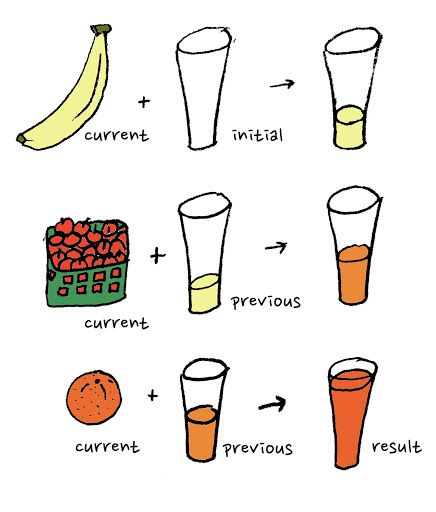
Fold高阶函数
输入一个列表,二元函数f,和初值init
输出一个元素,结果为列表每个元素与二元函数递归调用后的结果
Map/Filter/Fold
高阶函数
Richard Waters (1979) developed a program that automatically analyzes traditional Fortran programs, viewing them in terms of maps, filters, and accumulations. He found that fully 90 percent of the code in the Fortran Scientific Subroutine Package fits neatly into this paradigm. One of the reasons for the success of Lisp as a programming language is that lists provide a standard medium for expressing ordered collections so that they can be manipulated using higher-order operations. The programming language APL owes much of its power and appeal to a similar choice. In APL all data are represented as arrays, and there is a universal and convenient set of generic operators for all sorts of array operations.
— Conor Hoekstra
消除for循环(Sobol Sequence)
SUBROUTINE example ( D, N, M, dirVs, ret )
INTEGER i, j, k, D, N, M, len
INTEGER ia(M), ret(D,N), dirVs(M,D)
DO i = 1, N
len = 0
DO k = 1, M
IF( test(i,k) ) THEN
len = len + 1
ia(len) = k
ENDIF ENDDO
DO j = 1, D
ret(j, i) = 0
DO k = 1, len
ret(j,i) = ret(j,i) XOR dirVs(ia(k), j)
ENDDO
IF(i .GT. 1)
ret(j,i) = ret(j,i) XOR ret(j,i-1)
ENDDO
ENDDO ENDexample n m dirVs = -- d×m n×d
let lbody i = (let ia = filter (test i) [0..m-1]
xorV v = fold xor 0 [v!j| j<-ia]
in map xorV dirVs)
ret = map lbody [1..n]
e = replicate (length dirVs) 0
in tail (scan (zipWith xor) e ret)Map实现
template<typename IN, template <typename> class F> (1)
struct Map; (2)
template<template <typename> class F, typename ...Ts>
struct Map<TypeList<Ts...>, F> {
using type = TypeList<typename F<Ts>::type...>; (3)
};
template<typename IN, template <typename> class F>
using Map_t = typename Map<IN, F>::type;| 1 | 输入类型参数 IN 和 元函数 F |
| 2 | 声明一个元函数Map |
| 3 | 模式匹配当IN类型为TypeList时,对其每个 Ts… 元素进行元函数调用 |
1. template <typename> class F 为元函数声明,表示该函数输入一个类型参数2. typename F<Ts>::type 表示对元函数 F 调用,输入一个类型参数 Ts,返回调用后的类型参数 ::type3. typename F<Ts>::type… 展开后结果为 typename F<T1>::type, typename F<T2>::type, typename F<T3>::type, … |
Filter实现
template<typename IN, template <typename> class P, typename OUT = TypeList<>> (1)
struct Filter { using type = OUT; }; (2)
template<template <typename> class P, typename OUT, typename H, typename ...Ts>
struct Filter<TypeList<H, Ts...>, P, OUT>:
std::conditional_t<P<H>::value,
Filter<TypeList<Ts...>, P, typename OUT::template append<H>>,
Filter<TypeList<Ts...>, P, OUT>> { }; (3)
template<typename IN, template <typename> class P>
using Filter_t = typename Filter<IN, P>::type;| 1 | 输入类型参数 IN 和 谓词函数 P |
| 2 | 默认返回类型为空 TypeList; 列表为空时递归终止返回当前 OUT TypeList |
| 3 | 对当前列表第一个参数 H 进行 P 函数调用,根据真假判断要不要把结果放到 OUT TypeList |
| 1. Filter实现采用了尾递归方式,可能有助于编译器提高编译速度 2. 使用继承方式省去了写 using type = … 的代码3. P<H>::value 表示对元函数P的调用,输入一个类型参数 H,输出其布尔值 ::value4. 对 OUT TypeList进行append参数 H,因为 append 也是个模板元函数,内嵌于类TypeList中,需要写成 typename OUT::template append<H> ,可以看成是 out.append(h) 形式 |
Fold实现
template<typename IN, typename INIT, template<typename, typename> class OP> (1)
struct Fold { using type = INIT; }; (2)
template<typename IN, typename INIT, template<typename, typename> class OP>
using Fold_t = typename Fold<IN, INIT, OP>::type;
template<typename ACC, template<typename, typename> class OP,
typename H, typename ...Ts>
struct Fold<TypeList<H, Ts...>, ACC, OP>:
Fold<TypeList<Ts...>, typename OP<ACC, H>::type, OP> {}; (3)| 1 | 输入类型参数 IN,初始类型参数 INIT, 二元函数 OP |
| 2 | 默认返回初值;列表为空时递归终止返回当前 INIT 参数 |
| 3 | 对当前参数 H 执行二元函数 OP, 其返回类型更新 INIT 参数 |
1. template <typename, typename> class OP 为元函数声明,两个 typename 说明该函数输入两个类型参数2. typename OP<ACC, H>::type 表示对元函数 OP 调用,输入两个类型参数 ACC, H ,返回调用后的类型参数 ::type |
TypeList实战
连接两个TypeList:
Concat判断类型是否在TypeList中:
ElemTypeList去重:
Unique快速排序:
QuickSort求图全局最短路径,动静结合
构建TaskDSL
Concat
连接两个TypeList
template<typename IN, typename IN2> (1)
class Concat {
template<typename ACC, typename E> (2)
struct Append: ACC::template append<E> { };
public:
using type = Fold_t<IN2, IN, Append>; (3)
};
template<typename IN, typename IN2>
using Concat_t = typename Concat<IN, IN2>::type;| 1 | 输入两个TypeList: IN, IN2 |
| 2 | 定义 Append 二元操作输入两个参数,一个 ACC TypeList,一个类型参数 E,通过调用TypeList的 append 元函数 |
| 3 | Fold 高阶函数调用,输入 IN2,初值IN,二元操作 Append,对IN2 TypeList的每个元素进行 Append 调用 |
如何调用
Concat_t<TypeList<int, char>, TypeList<float>> // TypeList<int, char, float>Concat 2
有没有其他解法
template<typename IN, typename IN2>
struct Concat;
template<typename ...Ts, typename ...Ts2>
struct Concat<TypeList<Ts...>, TypeList<Ts2...>> { (1)
using type = TypeList<Ts..., Ts2...>; (2)
};
template<typename IN, typename IN2>
using Concat_t = typename Concat<IN, IN2>::type;| 1 | 模式匹配两个TypeList,得到各自模板参数包 Ts, Ts2 |
| 2 | 结果为两个TypeList的参数包都展开后放到一起 |
Concat 3
还有没有其他解法
template<typename IN, typename IN2>
struct Concat: IN2::template exportTo<IN::template append> { }; (1)
template<typename IN, typename IN2>
using Concat_t = typename Concat<IN, IN2>::type;| 1 | 使用参数转发函数exportTo,将IN2的参数转发到IN的append函数上去 |
| 1. 这里将exportTo当做高阶函数使用,其输入一个函数 IN::append,将自身的参数转调到这个函数上 2. 由于IN是模板类型参数,append 又是模板元函数,需要写成 IN::template append |
Elem
判断类型是否在TypeList中
template<typename IN, typename E> (1)
class Elem {
template<typename ACC, typename T>
struct FindE: std::conditional_t<ACC::value, ACC, std::is_same<T, E>> {} ; (2)
using Found = Fold_t<IN, std::false_type, FindE>; (3)
public:
constexpr static bool value = Found::value; (4)
};
template<typename IN, typename E>
constexpr bool Elem_v = Elem<IN, E>::value;| 1 | 输入两个类型参数:IN TypeList, 待查找类型E |
| 2 | 定义二元操作FindE,若ACC为真则说明已经找到过,直接返回;否则判断当前类型参数是否与E相等 |
| 3 | Fold 操作,输入IN TypeList,初值类型为false_type,二元操作FindE |
| 4 | 从布尔类型得到其值 |
如何调用
Elem_v<TypeList<int>, int>; // true
Elem_v<TypeList<int>, float>; // falseElem 2
还有没有其他解法
template<typename IN, typename E>
struct Elem {
constexpr static bool value = false; (1)
};
template<typename E, typename ...Ts>
struct Elem<TypeList<Ts...>, E> {
constexpr static bool value = (std::is_same_v<E, Ts> || ...); (2)
};
template<typename IN, typename E>
constexpr bool Elem_v = Elem<IN, E>::value;| 1 | 默认认为E不存在于IN中 |
| 2 | 模式匹配,若IN类型为TypeList,则其一个个类型与E匹配 |
得益于C++17的折叠表达式(fold expression): (pack op … ),使这种方式可行 |
Unique
对TypeList去重操作
template<typename IN> (1)
class Unique {
template<typename ACC, typename E> (2)
struct Append: std::conditional_t<Elem_v<ACC, E>, (3)
ACC, typename ACC::template append<E>> {};
public:
using type = Fold_t<IN, TypeList<>, Append>; (4)
};
template<typename IN>
using Unique_t = typename Unique<IN>::type;| 1 | 输入待去重的IN TypeList |
| 2 | 定义二元操作Append,输入ACC TypeList和待插入类型参数E |
| 3 | 当前仅当E不存在于ACC中插入列表 |
| 4 | Fold 高阶函数调用,输入待去重的IN TypeList,初值空表,二元操作 Append,对IN TypeList的每个元素进行 Append 调用 |
QuickSort
选取表中Pivot元素,以Pivot为划分点 Filter操作
小于Pivot的所有元素放到左边形成新表
大于等于Pivot的所有元素放到右边形成新表
对左右两个表进行递归QuickSort操作后,连接成表得到最终有序表 Fold操作
{40, 80, 30, 90, 10, 70, 50}
{{30, 10}, 40, {80, 90, 70, 50}}
{{{10}, 30}, 40, {80, 90, 70, 50}}
{{{10}, 30}, 40, {{70, 50}, 80, {90}}}
{{{10}, 30}, 40, {{{50}, 70}, 80, {90}}}
{10, 30, 40, 50, 70, 80, 90}
QuickSort
template<typename IN, template<typename, typename> class CMP> (1)
struct QuickSort { using type = TypeList<>; }; (2)
template<typename IN, template<typename, typename> class CMP>
using QuickSort_t = typename QuickSort<IN, CMP>::type;
template<template<typename, typename> class CMP, typename PIVOT, typename ...Ts>
class QuickSort<TypeList<PIVOT, Ts...>, CMP> {
using tails = TypeList<Ts...>;
template<typename E>
struct LT { constexpr static bool value = CMP<E, PIVOT>::value; }; (3)
template<typename E>
struct GE { constexpr static bool value = !CMP<E, PIVOT>::value; }; (3)
using SmallerSorted = QuickSort_t<Filter_t<tails, LT>, CMP>; (4)
using BiggerSorted = QuickSort_t<Filter_t<tails, GE>, CMP>; (4)
public:
using type = Concat_t<typename SmallerSorted::template append<PIVOT>, BiggerSorted>; (5)
};| 1 | 输入一个IN TypeList,比较元函数CMP |
| 2 | 默认返回空列表 |
| 3 | 定义两个元函数LT/GT,用于得到和PIVIOT比较结果 |
| 4 | Filter 操作得到左右两个表,对两个表进行递归QuickSort操作 |
| 5 | 连接成表得到最终有序表 |
QuickSort
如何调用
template<typename LHS, typename RHS> (1)
struct SizeCmp {
constexpr static bool value = sizeof(LHS) < sizeof(RHS); (1)
};
QuickSort_t<
TypeList<char, float, double, int, char>,
SizeCmp> // TypeList<char, char, float, int, double>>| 1 | 定义比较函数,输入两个类型,根据类型大小排序 |
全局最短路径
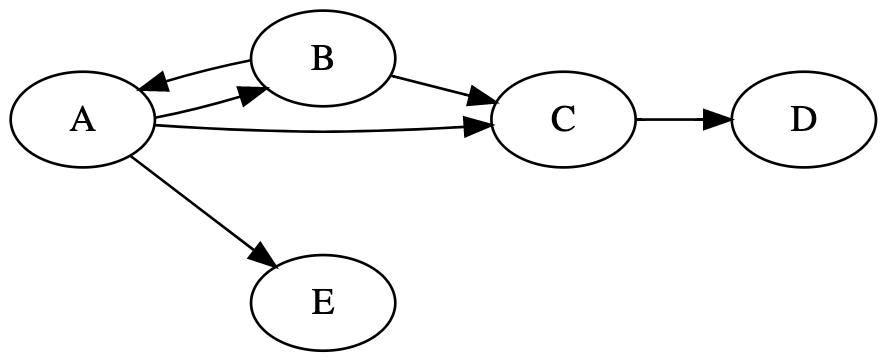
存在环:A→B→A
A→D最短路径其实是A→C→D
D→E不可达
伪代码
任意给定两个点,采用深度优先搜索,伪代码如下
def find_shortest_path(from, to, path = []): (1)
if from == to: return path # reach target (2)
if from in path: return [] # find cycle (3)
for each (from, v) in edges: # expand next nodes (4)
cur_path = from + find_shortest_path(v, to) (5)
path = min(path, cur_path) (6)
return path| 1 | 输入起点from, 终点to |
| 2 | 若找到目的地to,返回当前路径 |
| 3 | 若当前点存在当前路径中,则遇到了环,返回空路径 |
| 4 | 从边集edges找到当前点from的邻接边表 Filter操作 从邻接边表得到邻接点表v Map操作 |
| 5 | 更新当前路径curr_path |
| 6 | 求出最短非空路径 Fold操作 |
用户界面
template<char ID>
struct Node { constexpr static char id = ID; };
using A = Node<'A'>;
using B = Node<'B'>;
using C = Node<'C'>;
using D = Node<'D'>;
using E = Node<'E'>;
using g = Graph< (1)
link(node(A) -> node(B) -> node(C) -> node(D)),
link(node(A) -> node(C)), // test shortest path: A -> C -> D
link(node(B) -> node(A)), // test cycle
link(node(A) -> node(E))>; // test D -> E unreachable
static_assert(g::getPath('A', 'D').sz == 3); // compile-time test (2)
auto path = g::getPath(argv[1][0], argv[2][0]); // runtime test (2)
std::cout << " path size: " << path.sz << std::endl;| 1 | 用户构造边集,返回Graph对象 |
| 2 | Graph对象生成的getPath接口既能用于编译时,也能运行时 |
构造边集
using g = Graph< (1)
link(node(A) -> node(B) -> node(C) -> node(D)),
link(node(A) -> node(C)), // test shortest path: A -> C -> D
link(node(B) -> node(A)), // test cycle
link(node(A) -> node(E))>; // test D -> E unreachableusing g = Graph<
auto(*)(A) -> auto(*)(B) -> auto(*)(C) -> auto(*)(D) -> void,
auto(*)(A) -> auto(*)(C) -> void,
auto(*)(B) -> auto(*)(A) -> void,
auto(*)(A) -> auto(*)(E) -> void>;auto(*)(A) → B 声明一个函数指针类型,为 后置返回类型 写法,通过在前面声明 auto ,这样返回类型就可以通过箭头→写到后面 |
| 1. 为了更好描述图,正好用上 后置返回类型 中的箭头符号 2. 由于函数可以返回一个函数,所以可以串起来,达到链 auto(*)(A) → auto(*)(B) → auto(*)(C) → auto(*)(D) → void 效果3. 约定链条最后用 void 表示结束 |
边结构
template<typename F, typename T>
struct Edge {
using From = F;
using To = T;
};基础操作
template<typename Node = void>
struct EdgeTrait {
template<typename Edge> struct IsFrom (1)
{ constexpr static bool value = std::is_same_v<typename Edge::From, Node>; };
template<typename Edge> struct IsTo (1)
{ constexpr static bool value = std::is_same_v<typename Edge::To, Node>; };
template<typename Edge> (2)
struct GetFrom { using type = typename Edge::From; };
template<typename Edge> (2)
struct GetTo { using type = typename Edge::To; };
};| 1 | 输入一个节点Node,一条边Edge,输出该节点是否为Edge的源From、目的点To |
| 2 | 输入一条边Edge,输出它的源From、目的点To |
| 约定用 Trait 后缀表明为一组类型的属性、动作 |
解构链Chain
链 auto(*)(A) → auto(*)(B) → auto(*)(C) → auto(*)(D) → void
Edge边表 TypeList<Edge<A, B>, Edge<B, C>, Edge<C, D>>
定义一个解构函数Chain,输入链,输出Edge表
template<typename T, typename OUT = TypeList<>>
struct Chain;
template<typename F, typename OUT>
struct Chain<auto(*)(F) -> void, OUT> {
using From = F;
using type = OUT; (1)
};
template<typename F, typename T, typename OUT>
struct Chain<auto(*)(F) -> T, OUT> {
private:
using To = typename Chain<T, OUT>::From;
public:
using From = F;
using type = typename Chain<T,
typename OUT::template append<Edge<From, To>>>::type; (2)
};| 1 | 递归边界情况,当遇到链尾 void ,返回当前边表 |
| 2 | 常规情况,不断构造Edge边,存到边表OUT TypeList中 |
获得边集
template<typename... Chains> (1)
class Graph {
using Edges = Fold_t< (2)
TypeList<typename Chain<Chains>::type...>,
TypeList<>,
Concat>;
...
};| 1 | 用户输入链条集 |
| 2 | Chain元函数解构每一条链条得到边表的集合,通过 Fold 操作展开得到边集 |
两点间最短路径
元函数PathFinder声明如下
// def find_shortest_path(from, to, path = []):
template<typename FROM, typename TARGET, (1)
typename PATH = TypeList<>, typename = void> (2)
struct PathFinder;| 1 | 输入两个点FROM,TARGET,输出他们之间最短路径 |
| 2 | PATH路径用于判断是否遇到了环;第四个参数用于模式匹配中的条件判断 |
有时候 typename Cond = void 对类型参数名 Cond 不关注时,可以写成 typename = void |
两点间最短路径
// if from == to: return path # reach target
template<typename TARGET, typename PATH>
struct PathFinder<TARGET, TARGET, PATH>: (1)
PATH::template append<TARGET> { }; (2)| 1 | 模式匹配,当FROM == TARGET时,到达终点 |
| 2 | 返回最短路径 |
// if from in path: return [] # find cycle
template<typename CURR_NODE, typename TARGET, typename PATH>
struct PathFinder<CURR_NODE, TARGET, PATH,
std::enable_if_t<Elem_v<PATH, CURR_NODE>>>: (1)
TypeList<> {}; // return empty path (2)| 1 | 模式匹配,当CURR_NODE出现在当前路径中,说明遇到了环 |
| 2 | 返回空路径 |
两点间最短路径
template<typename CURR_NODE, typename TARGET, typename PATH>
class PathFinder<CURR_NODE, TARGET, PATH,
std::enable_if_t<! std::is_same_v<CURR_NODE, TARGET>
&& !Elem_v<PATH, CURR_NODE>>> { (1)
using EdgesFrom = Filter_t<Edges, EdgeTrait<CURR_NODE>::template IsFrom>; (2)
// for each (from, v) in edges: # expand next nodes
using NextNodes = Map_t<EdgesFrom, EdgeTrait<>::GetTo>; (3)
// cur_path = from + find_shortest_path(v, to)
template<typename NEXT_NODE>
struct GetPath: PathFinder<NEXT_NODE, TARGET,
typename PATH::template append<CURR_NODE>> {};
using AllPaths = Map_t<NextNodes, GetPath>; (4)
template<typename ACC, typename Path> struct MinPath:
std::conditional_t<(ACC::size == 0 ||
((ACC::size > Path::size) && Path::size > 0)), Path, ACC> {};
public:
// path = min(path, cur_path)
using type = Fold_t<AllPaths, TypeList<>, MinPath>; (5)
};| 1 | 模式匹配,当前仅当当前CURR_NODE节点不是终点TARGET,并且不是环时 |
| 2 | Filter 操作,从边集Edges找出邻接CURR_NODE边 |
| 3 | Map 操作,对边表每一条边进行GetTo操作,获取CURR_NODE邻接点表 |
| 4 | Map 操作,对每个邻接点做为起点进行递归求最短路径集 |
| 5 | Fold 操作,对每条可行路径,找出最短的那条作为最短路径 |
动静结合
运行时如何求最短路径
编译期生成所有节点间的最短路径
提供接口供运行时查表,输入起点、终点,查出最短路径
如何得到所有节点间的组合
对边集的起点表和邻接点表做笛卡尔积!
{A→B, B→C} {A, B} x {B, C} {(A, B), (A, C), (B, B), (B, C)}
笛卡尔积
输入两个列表,对两个列表中的元素两两组合得到序对表
template<typename A, typename B,
template<typename, typename> class PAIR>
struct CrossProduct;
template<typename A, typename B, template<typename, typename> class PAIR>
using CrossProduct_t = typename CrossProduct<A, B, PAIR>::type;
template<typename A, typename B, template<typename, typename> class PAIR>
class CrossProduct {
template<typename RESULT_OUTTER, typename TA> (1)
struct OuterAppend {
template<typename RESULT_INNER, typename TB> (2)
struct InnerAppend: RESULT_INNER::template append<PAIR<TA, TB>> { };
using type = Fold_t<B, RESULT_OUTTER, InnerAppend>;
};
public:
using type = Fold_t<A, TypeList<>, OuterAppend>;
};| 1 | 外层循环,得到类型参数TA |
| 2 | 内层循环,得到类型参数TB,两两组合成序对PAIR<TA, TB>,放到RESULT表中 |
路径存储
枚举出所有节点间的组合情况
using AllPairs = CrossProduct_t<
Unique_t<Map_t<Edges, EdgeTrait<>::GetFrom>>,
Unique_t<Map_t<Edges, EdgeTrait<>::GetTo>>,
std::pair>;路径数据结构
template<typename NODE_TYPE>
struct Path {
const NODE_TYPE* path;
size_t sz;
};
template<typename NODE, typename... NODEs>
class PathStorage { (1)
using NODE_TYPE = std::decay_t<decltype(NODE::id)>;
constexpr static NODE_TYPE pathStorage[] { NODE::id, NODEs::id... };
public:
constexpr static Path<NODE_TYPE> path {
.path = pathStorage,
.sz = sizeof...(NODEs) + 1,
};
};| 1 | PathStorage<A, B, C>::path 存储 A→C 之间最短路径 |
最短路径表
我们期望编译期生成如下表,供运行时查询
FROM | DST | MinPath |
A | B | PathStorage<A, B>::path |
A | C | PathStorage<A, C>::path |
A | D | PathStorage<A, C, D>::path |
A | A | PathStorage<A>::path |
A | E | PathStorage<A, E>::path |
表项数据结构:PATH_PAIR: std::pair<PAIR, PATH> ⇒ std::pair<std::pair<FROM, DST>, PATH>
生成路径
输入两节点序对PAIR,输出PATH_PAIR,Map 操作
template<typename PAIR>
struct GetPath {
using type = std::pair<PAIR,
typename PathFinder<typename PAIR::first_type,
typename PAIR::second_type>::type>;
};
using AllPaths = Map_t<AllPairs, GetPath>;删除空路径项,Filter 操作
template<typename PATH_PAIR>
struct IsNonEmptyPath {
constexpr static bool value = (PATH_PAIR::second_type::size > 0);
};
using AllNonEmptyPaths = Filter_t<AllPaths, IsNonEmptyPath>;生成数据表项
Map 操作
template<typename PATH_PAIR>
struct SavePath {
using type = std::pair<typename PATH_PAIR::first_type,
typename PATH_PAIR::second_type::template exportTo<PathStorage>>; (1)
};
using SavedPaths = Map_t<AllNonEmptyPaths, SavePath>; (2)| 1 | 路径数据转发至 PathStorage 类,触发存储 |
| 2 | SavedPath即最短路径表 |
生成编译时、运行时接口
template<typename NODE_TYPE, typename FROM, typename TARGET, typename PATH>
constexpr static bool matchPath(NODE_TYPE from, NODE_TYPE to,
Path<NODE_TYPE>& result, std::pair<std::pair<FROM, TARGET>, PATH>) {
if (FROM::id == from && TARGET::id == to) { (1)
result = PATH::path; (1)
return true;
}
return false;
}
template<typename NODE_TYPE, typename ...PATH_PAIRs>
constexpr static void matchPath(NODE_TYPE from, NODE_TYPE to,
Path<NODE_TYPE>& result, TypeList<PATH_PAIRs...>) {
(matchPath(from, to, result, PATH_PAIRs{}) || ...); (2)
}// export compile/run-time interface
template<typename NODE_TYPE>
constexpr static Path<NODE_TYPE> getPath(NODE_TYPE from, NODE_TYPE to) { (3)
Path<NODE_TYPE> result{};
matchPath(from, to, result, SavedPaths{});
return result;
}| 1 | 当FROM/TARGET与表项匹配时,返回路径 result |
| 2 | 遍历查表动作,直到找到路径为止 |
| 3 | 供运行时使用 |
最终效果
template<char ID>
struct Node { constexpr static char id = ID; };
using A = Node<'A'>;
using B = Node<'B'>;
using C = Node<'C'>;
using D = Node<'D'>;
using E = Node<'E'>;
using g = Graph<
link(node(A) -> node(B) -> node(C) -> node(D)),
link(node(A) -> node(C)), // test shortest path: A -> C -> D
link(node(B) -> node(A)), // test cycle
link(node(A) -> node(E))>; // test D -> E unreachable
static_assert(g::getPath('A', 'D').sz == 3); // compile-time test
auto path = g::getPath(argv[1][0], argv[2][0]); // runtime test
std::cout << " path size: " << path.sz << std::endl;构建TaskDSL
tf::Executor executor;
tf::Taskflow taskflow("simple");
auto A = taskflow.emplace([]() { std::cout << "TaskA\n"; }); // +---+
auto B = taskflow.emplace([]() { std::cout << "TaskB\n"; }); // +---->| B |-----+
auto C = taskflow.emplace([]() { std::cout << "TaskC\n"; }); // | +---+ |
auto D = taskflow.emplace([]() { std::cout << "TaskD\n"; }); // +---+ +-v-+
// | A | | D |
A.precede(B); // B runs after A // +---+ +-^-+
A.precede(C); // C runs after A // | +---+ |
B.precede(D); // D runs after B // +---->| C |-----+
C.precede(D); // D runs after C // +---+
executor.run(taskflow).wait();tf::Executor executor;
tf::Taskflow taskflow("simple");
def_task((A), { std::cout << "TaskA\n"; }); // +---+
def_task((B), { std::cout << "TaskB\n"; }); // +---->| B |-----+
def_task((C), { std::cout << "TaskC\n"; }); // | +---+ |
def_task((D), { std::cout << "TaskD\n"; }); // +---+ +-v-+
// | A | | D |
taskbuild( // +---+ +-^-+
task(A) // | +---+ |
->fork(B, C) // +---->| C |-----+
->task(D) // +---+
)(taskflow);
executor.run(taskflow).wait();TaskDSL: Context
int counter;
struct Context {
int &rcounter; // use counter(borrow)
} context{counter};
def_task((A, Context), { rcounter=0; });
def_task((B, Context), { rcounter++; });
def_task((C, Context), {
if (rcounter != 5) std::cout << "loops again (goes to B)\n"; return 0;
std::cout << "breaks the loop (goes to D)\n"; return 1;
});
def_task((D, Context), { std::cout << "done with counter equal to " << rcounter << '\n'; });
auto tasks = taskbuild(
task(A) -> task(B) -> task(C),
task(C) -> fork(B, D)
)(taskflow, context);语言发展完善体验
模板元编程
1986 C++引入模板
C++98 模板实例化
C++11 模板类别名、可变模板参数、static_assert、decltype、type_traits
C++14 常量模板、decltype(auto)、integer_sequence
C++17 折叠表达式、CTAD、auto非类型参数、void_t
C++20 Concept、lambda模板参数
constexpr
C++11 引入constexpr简单函数
C++14 放开constexpr约束, 模板变量
C++17 if constexpr、constexpr lambda
C++20 constexpr容器、constexpr new、constexpr try-catch、constexpr虚函数、consteval/constinit
constexpr STL algorithms
结论
库、框架开发者必备技能
更高级别抽象层次,实现零成本抽象
设计灵活组合、类型安全、容易使用的接口
领域特定语言DSL